Qismən diferensial tənliklər (PDE) çox dəyişənlərin qarşılıqlı əlaqəsini təmsil edən riyazi problemlər sinfidir və buna görə də mürəkkəb fiziki sistemlərə gəldikdə proqnozlaşdırıcı gücə malikdir. Bu tənliklərin həlli daimi problemdir və bunu etmək üçün mövcud hesablama üsulları vaxt aparan və bahalıdır.

İndi, Yuta Universitetinin Con və Marcia Price Mühəndislik Kollecinin tədqiqatları bu prosesi sürətləndirməyin bir yolunu göstərir: bu tənlikləri işıqda kodlamaq və onları yeni dizayn edilmiş “optik sinir mühərrikinə” və ya BİR-ə qidalandırmaq.

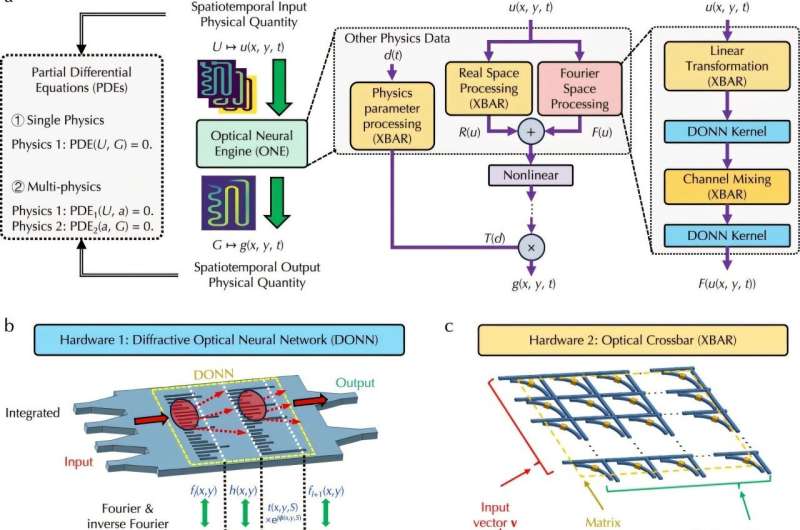
Tədqiqatçıların ONE-si diffraktiv optik neyron şəbəkələri və optik matris çarpanlarını birləşdirir. Tədqiqatçılar PDE-ləri rəqəmsal şəkildə təmsil etmək əvəzinə, onları optik olaraq, işıq dalğasının intensivliyi və fazası kimi müxtəlif xüsusiyyətləri ilə təmsil olunan dəyişənlərlə təmsil etdilər. Dalğa BİR-in optik komponentləri seriyasından keçdikcə, bu xüsusiyyətlər, nəticədə verilmiş PDE-nin həllini təmsil edənə qədər tədricən dəyişir və dəyişir.

Tədqiqata Elektrik və Kompüter Mühəndisliyi Departamentinin dosenti Weilu Gao və Ph.D Ruiyang Chen rəhbərlik edirdi. Gao tədqiqat qrupunun namizədi. Onlar Nature Communications jurnalında bu optik sinir mühərrikini nümayiş etdirən bir araşdırma dərc etdilər .

“Qismən diferensial tənliklər bahalı və çox vaxt aparan real təcrübələr yerinə yetirmək əvəzinə fizika problemlərini simulyasiya etmək üçün güclü hesablama vasitəsidir” dedi Çen. “Lakin indiki ədədi simulyasiya üsulu yavaşdır və çoxlu hesablama resursları tələb edir və hətta elektron maşın öyrənmə üsulları kifayət qədər sürətli deyil.”

Hazırda PDE-ləri həll etmək üçün istifadə olunan maşın öyrənmə üsulları və rəqəmsal neyron şəbəkələri tənliyin hesablama qovşaqları şəbəkəsi vasitəsilə ötürülməsini nəzərdə tutur, hər biri növbəti qovşaqdan ötürərkən çıxışını ağırlaşdırır. Siqnal şəbəkədən keçdikdə, düzgün həll ən çox çəkiyə çevrilir və çıxış kimi başa çatır.

https://googleads.g.doubleclick.net/pagead/ads?gdpr=0&us_privacy=1—&gpp_sid=-1&client=ca-pub-0536483524803400&output=html&h=280&slotname=2793866484&adk=2520359048&adf=1100001614&pi=t.ma~as.2793866484&w=750&abgtt=6&fwrn=4&fwrnh=0&lmt=1749620140&rafmt=1&armr=3&format=750×280&url=https%3A%2F%2Ftechxplore.com%2Fnews%2F2025-06-optical-neural-partial-differential-equations.html&fwr=0&rpe=1&resp_fmts=3&wgl=1&uach=WyJXaW5kb3dzIiwiMTkuMC4wIiwieDg2IiwiIiwiMTM3LjAuNzE1MS4xMDMiLG51bGwsMCxudWxsLCI2NCIsW1siR29vZ2xlIENocm9tZSIsIjEzNy4wLjcxNTEuMTAzIl0sWyJDaHJvbWl1bSIsIjEzNy4wLjcxNTEuMTAzIl0sWyJOb3QvQSlCcmFuZCIsIjI0LjAuMC4wIl1dLDBd&dt=1749620139458&bpp=1&bdt=934&idt=686&shv=r20250609&mjsv=m202506090101&ptt=9&saldr=aa&abxe=1&cookie=ID%3Dfdc40d724f2dca57%3AT%3D1735367325%3ART%3D1749620139%3AS%3DALNI_MYStQ6fUQQQLyo5Z7z1h-XhXcWBtA&gpic=UID%3D00000f80eacffadc%3AT%3D1735367325%3ART%3D1749620139%3AS%3DALNI_MYaOugky0UawScoidzfbXof3-N-iw&eo_id_str=ID%3De43bb863646b60b8%3AT%3D1735367325%3ART%3D1749620139%3AS%3DAA-AfjbQoPwZqH28q9IwcCLRSzzg&prev_fmts=0x0&nras=1&correlator=6053272677681&frm=20&pv=1&rplot=4&u_tz=240&u_his=1&u_h=1080&u_w=1920&u_ah=1032&u_aw=1920&u_cd=24&u_sd=1&dmc=8&adx=448&ady=1874&biw=1905&bih=945&scr_x=0&scr_y=0&eid=31092898%2C31092913%2C42532523%2C95353386%2C95362655%2C31092908%2C95362799%2C95359265%2C95362802%2C95363072%2C95360684&oid=2&pvsid=1780841492453462&tmod=731885669&uas=0&nvt=1&ref=https%3A%2F%2Fphys.org%2F&fc=1920&brdim=0%2C0%2C0%2C0%2C1920%2C0%2C1920%2C1032%2C1920%2C945&vis=1&rsz=%7C%7CpeEbr%7C&abl=CS&pfx=0&fu=128&bc=31&bz=1&td=1&tdf=2&psd=W251bGwsbnVsbCxudWxsLDNd&nt=1&ifi=2&uci=a!2&btvi=1&fsb=1&dtd=1492

Tədqiqatçıların ONE bu konsepsiyanı götürür və fotonik cihazlara tətbiq edir.

“BİR, mövqelərin və zamanın funksiyası kimi çıxış fiziki kəmiyyətinin məkan-zaman məlumatlarını proqnozlaşdırmaq üçün mövqelərin və zamanın funksiyası olan giriş fiziki kəmiyyətinin məkan-zaman məlumatlarını götürür” dedi Gao.

Elektron maşın öyrənmə üsulları oxşar nəticə verə bilər, lakin daha yavaş sürətlə və daha yüksək enerji xərcləri ilə.

“Bu optik yanaşma maşın öyrənmə prosesini sürətləndirir və elektron yanaşma ilə müqayisədə daha az enerji tələb edir” dedi aparıcı müəllif və keçmiş Gao laboratoriya üzvü Yingheng Tang, hazırda Lawrence Berkeley Milli Laboratoriyasının tədqiqatçısı.

Tədqiqatçılar ONE-nin imkanlarını bir sıra PDE-lərdə, o cümlədən Darsi axını tənliyi, maqnitsizləşmədə maqnitostatik Puasson tənliyi və sıxılmayan mayedə Navier-Stokes tənliyi də nümayiş etdirdilər.

“Darsi axını tənliyi, məsələn, məsaməli bir mühitdən keçən maye axınını təsvir edir” dedi Gao. “Verilmiş mühitin içindəki keçiricilik və təzyiq sahələri haqqında məlumatları nəzərə alaraq, ONE arxitekturası mahiyyətcə bu keyfiyyətlər arasındakı xəritəni öyrənir və təcrübə etmədən axın xüsusiyyətlərini proqnozlaşdıra bilir.”

“Bu tədqiqat geologiya və çip dizaynı kimi genişmiqyaslı elmi və mühəndis hesablamaları üçün çox yönlü və güclü platforma təklif edir” dedi Gao.

Daha çox məlumat: Yingheng Tang et al, Elmi qismən diferensial tənliklərin həlli üçün optik sinir mühərriki, Nature Communications (2025). DOI: 10.1038/s41467-025-59847-3

Jurnal məlumatı: Nature Communications Yuta Universiteti tərəfindən təmin edilmişdir