Anderson keçidi nizamsız sistemlərdə baş verən, diffuziya vəziyyətindən (yəni, dalğaların və ya hissəciklərin yayıldığı) lokallaşdırılmış vəziyyətə, onların müəyyən bölgələrdə tutulduğu vəziyyətə keçidi nəzərdə tutan faza keçididir. Bu vəziyyət ilk dəfə nizamsız bərk cisimlərdə elektronların düzülməsini tədqiq edən fizik Philip W. Anderson tərəfindən tədqiq edilmiş, lakin sonradan bunun işığın və digər dalğaların yayılmasına da aid olduğu aşkar edilmişdir.

Missuri Elm və Texnologiya Universiteti, Yale Universiteti və Fransadakı Qrenobl Alpes Universitetinin tədqiqatçıları bu yaxınlarda 3D nizamsız sistemlərdə işıq (yəni, elektromaqnit dalğaları) üçün Anderson keçidini daha da araşdırmaq üçün yola çıxdılar.

Onların Physical Review Letters jurnalında dərc olunmuş məqaləsi , elektromaqnit dalğalarını əks etdirən materialların, mükəmməl elektrik keçirici (PEC) sferalarının düzülüşündə işıq dalğalarının nəqlinin simulyasiyasını təsvir edir.

“Bu məqalə Nature Physics- də əvvəlki nəşrimizə əsaslanır . O, Anderson tərəfindən 3D təsadüfi mühitdə işığın lokalizasiyasını (AL) nümayiş etdirdi, lakin diffuziyadan lokalizasiyaya keçidin necə baş verdiyini öyrənmədi” deyə məqalənin birinci müəllifi Aleksey Yamilov Phys.org-a bildirib.

“Anderson keçidinin əvvəlki tədqiqatlarına nizamsız bərk cisimlərdə elektronlar üçün model ədədi hesablamalar, mexaniki sistemlərdə vibrasiya, həmçinin soyuq atom sistemlərində ultrasəs və maddə dalğaları ilə təcrübələr daxildir. Onlar müəyyən kəmiyyətlərin tədqiq olunan fiziki sistemin fiziki təbiətindən asılı olmayaraq eyni davrandığını müəyyən etməklə keçidin universallığını nümayiş etdirdilər.”

Yamilov və onun həmkarları Hui Cao və Sergey Skipetrov əvvəlki araşdırmalarına əsaslanaraq Andersonun işıq üçün keçidinin digər dalğa növləri üçün müşahidə edilənlə eyni olduğunu nümayiş etdirməyə başladılar. Bunun üçün onlar əvvəlcə tədqiq etdikləri mühitdə diffuziyadan lokalizasiyaya keçidin əsl Anderson keçidini təmsil edib-etmədiyini müəyyən etməyə başladılar.

https://googleads.g.doubleclick.net/pagead/ads?gdpr=0&us_privacy=1—&gpp_sid=-1&client=ca-pub-0536483524803400&output=html&h=188&slotname=8188791252&adk=1687169288&adf=4054963813&pi=t.ma~as.8188791252&w=750&abgtt=6&fwrn=4&lmt=1739783943&rafmt=11&format=750×188&url=https%3A%2F%2Fphys.org%2Fnews%2F2025-02-simulations-reveal-anderson-transition-3d.html&wgl=1&uach=WyJXaW5kb3dzIiwiMTkuMC4wIiwieDg2IiwiIiwiMTMyLjAuNjgzNC4xOTciLG51bGwsMCxudWxsLCI2NCIsW1siTm90IEEoQnJhbmQiLCI4LjAuMC4wIl0sWyJDaHJvbWl1bSIsIjEzMi4wLjY4MzQuMTk3Il0sWyJHb29nbGUgQ2hyb21lIiwiMTMyLjAuNjgzNC4xOTciXV0sMF0.&dt=1739783939439&bpp=1&bdt=54&idt=107&shv=r20250211&mjsv=m202502120101&ptt=9&saldr=aa&abxe=1&cookie=ID%3Df22668bce9793ae4%3AT%3D1735196613%3ART%3D1739783743%3AS%3DALNI_Mb4Xpwl1SO1AcvqroR6xccDm_sheQ&gpic=UID%3D00000f7c5320f40b%3AT%3D1735196613%3ART%3D1739783743%3AS%3DALNI_Mb1dz_DHiT2yDzXLMaB9CDkQl4XGg&eo_id_str=ID%3Dcdf7f2f01784f52d%3AT%3D1735196613%3ART%3D1739783743%3AS%3DAA-Afjb8kbeupLLyQ0QHQmZxpM4v&prev_fmts=0x0%2C1903x945&nras=2&correlator=4379662316734&frm=20&pv=1&rplot=4&u_tz=240&u_his=3&u_h=1080&u_w=1920&u_ah=1032&u_aw=1920&u_cd=24&u_sd=1&dmc=8&adx=447&ady=2032&biw=1903&bih=945&scr_x=0&scr_y=0&eid=31090351%2C95352069%2C31090416%2C31090357%2C95347432%2C95350015&oid=2&pvsid=2014775389331252&tmod=684137592&uas=0&nvt=1&ref=https%3A%2F%2Fphys.org%2F&fc=1920&brdim=0%2C0%2C0%2C0%2C1920%2C0%2C0%2C0%2C1920%2C945&vis=1&rsz=%7C%7CpeEbr%7C&abl=CS&pfx=0&fu=128&bc=31&bz=0&td=1&tdf=2&psd=W251bGwsbnVsbCxudWxsLDNd&nt=1&ifi=2&uci=a!2&btvi=1&fsb=1&dtd=3834

Bundan əlavə, onlar iki rejimi ayıran kritik tezlikin (yəni, diffuziya və lokalizasiya) mövcudluğunu araşdırmaq istəyirdilər ki, bu da kəskin hərəkətlilik kənarı kimi istinad edilir.

Nəhayət, onlar keçidin universallığını müəyyən etmək üçün Anderson keçidinin lokalizasiya nəzəriyyəsi tərəfindən proqnozlaşdırılan universal miqyaslı davranışı nümayiş etdirmə dərəcəsini araşdırdılar.

Skipetrov izah etdi: “Təxminən 40 ildir ki, alimlərin işığın AL-ini müşahidə etdikdən sonra, Təbiət Fizikası məqaləmiz bu sualları çox aktual etdi”.

“Anderson keçidinin tədqiqi hər hansı bir faza keçidinin tədqiqi ilə eyni fundamental çətinliyi təqdim edir: o, yalnız sonsuz genişlikli sistemdə baş verir, bu, təcrübələrdə və ya ədədi simulyasiyalarda heç vaxt belə olmur . Sonlu ölçülü sistemdə kəskin keçid fasiləsiz krossoverlə əvəz olunur.”

Faza keçidlərini öyrənən əvvəlki tədqiqatlarda rast gəlinən çətinlikləri aradan qaldırmaq üçün tədqiqatçılar sonlu ölçülü miqyaslama yanaşmasından istifadə etdilər. Bu yanaşma onlara 3D sisteminin ölçüsü artdıqca diffuziya və lokalizasiya arasındakı keçidi yoxlamağa imkan verdi.

“Faza keçidlərini öyrənmək üçün hazırlanmış statistik fizikanın standart üsulları əldə edilən ölçüdən asılılıqdan sonsuz sistemdə müşahidə olunacaq keçid parametrlərini təyin etməyə imkan verir”, – deyə Yamilov bildirib.

“Çox güclü olsa da, bu yanaşma hələ də böyük (sonsuz olmasa da) ölçülü nümunələrdə işığın səpilməsini simulyasiya etməyi tələb edir ki, bu da FlexCompute, Inc tərəfindən hazırlanmış inqilabi proqram Tidy3D tərəfindən mümkün olmuşdur.”

Elektromaqnit dalğalarının davranışını simulyasiya etmək üçün istifadə edilə bilən proqram platforması olan Tidy3D-dən istifadə edən tədqiqatçılar Anderson keçid nöqtəsi yaxınlığında müxtəlif tezliklərdə 3D metal sistemin ölçüsü ilə yanaşı işığın ötürülməsinin necə dəyişdiyini öyrənməyə başladılar.

Gündəlik anlayışlar üçün Phys.org-a etibar edən 100.000-dən çox abunəçi ilə elm, texnologiya və kosmosda ən son yenilikləri kəşf edin . Pulsuz xəbər bülleteni üçün qeydiyyatdan keçin və mühüm nailiyyətlər, yeniliklər və tədqiqatlar haqqında gündəlik və ya həftəlik yeniləmələr əldə edin .Abunə ol

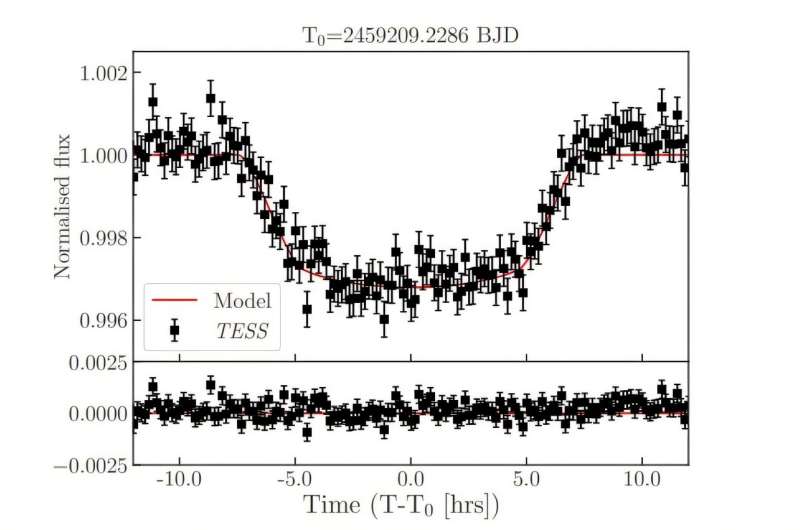
Onlar öz simulyasiyalarında metal konstruksiyalar vasitəsilə işıq impulsları göndərdilər və işığın nə dərəcədə keçdiyini ölçdülər. Bu, onlara kritik nöqtə kimi tanınan diffuziyadan lokalizasiyaya keçidin baş verdiyi dəqiq tezliyi müəyyən etməyə imkan verdi.

“Bu xüsusi nöqtədə müxtəlif sistem ölçüləri üçün ötürmə əyriləri hamısı bir-birini kəsir” dedi Yamilov.

“Əsas məsələ, əlbəttə ki, əvvəlki nəşrimizdə bildirdiyimiz kimi işığın Anderson lokalizasiyasını nümayiş etdirən bir sistemlə başlamaq idi. Sonra müasir hesablama metodlarından istifadə edərək, bunun nizamsız metallarda elektronlarla baş verənlərə bənzər, əsl faza keçidi olduğunu qəti şəkildə göstərmək üçün kifayət qədər böyük sistemləri simulyasiya etdik.”

Yamilov və onun həmkarları tərəfindən həyata keçirilən simulyasiyalar göstərdi ki, onların simulyasiya etdikləri 3D nizamsız sistemlərdə işığın keçidi digər Anderson keçidləri ilə eyni universallıq sinfinə aiddir. Bu o deməkdir ki, onlar elektron dalğalardan daha mürəkkəb olsalar belə, elektromaqnit dalğaları lokallaşdıqda eyni fundamental davranışı nümayiş etdirirlər.

“Son vaxtlara qədər işığın AL-ini müşahidə etmək və onu sistematik şəkildə öyrənmək üçün kifayət qədər ölçülü 3D sistemləri hesablama məhdudiyyətləri səbəbindən simulyasiya etmək mümkün deyildi”, – Yamilov bildirib.

“FlexCompute Inc tərəfindən irəli sürülən Sonlu Fərq Zaman Sahəsi (FDTD) alqoritmlərindəki son irəliləyişlər, nəhayət, belə simulyasiyaları aktivləşdirdi. İndi bunu hər kəs edə bilər! Əslində, kodumuz ictimaiyyət üçün açıqdır və FlexCompute Inc hər kəsə nəticələrimizi pulsuz yoxlamaq imkanı təklif etmişdir.”

https://googleads.g.doubleclick.net/pagead/ads?gdpr=0&us_privacy=1—&gpp_sid=-1&client=ca-pub-0536483524803400&output=html&h=188&slotname=8188791252&adk=1687169288&adf=3096487112&pi=t.ma~as.8188791252&w=750&abgtt=6&fwrn=4&lmt=1739783962&rafmt=11&format=750×188&url=https%3A%2F%2Fphys.org%2Fnews%2F2025-02-simulations-reveal-anderson-transition-3d.html&wgl=1&uach=WyJXaW5kb3dzIiwiMTkuMC4wIiwieDg2IiwiIiwiMTMyLjAuNjgzNC4xOTciLG51bGwsMCxudWxsLCI2NCIsW1siTm90IEEoQnJhbmQiLCI4LjAuMC4wIl0sWyJDaHJvbWl1bSIsIjEzMi4wLjY4MzQuMTk3Il0sWyJHb29nbGUgQ2hyb21lIiwiMTMyLjAuNjgzNC4xOTciXV0sMF0.&dt=1739783939440&bpp=1&bdt=55&idt=135&shv=r20250211&mjsv=m202502120101&ptt=9&saldr=aa&abxe=1&cookie=ID%3Df22668bce9793ae4%3AT%3D1735196613%3ART%3D1739783743%3AS%3DALNI_Mb4Xpwl1SO1AcvqroR6xccDm_sheQ&gpic=UID%3D00000f7c5320f40b%3AT%3D1735196613%3ART%3D1739783743%3AS%3DALNI_Mb1dz_DHiT2yDzXLMaB9CDkQl4XGg&eo_id_str=ID%3Dcdf7f2f01784f52d%3AT%3D1735196613%3ART%3D1739783743%3AS%3DAA-Afjb8kbeupLLyQ0QHQmZxpM4v&prev_fmts=0x0%2C1903x945%2C750x188%2C980x120&nras=3&correlator=4379662316734&frm=20&pv=1&rplot=4&u_tz=240&u_his=4&u_h=1080&u_w=1920&u_ah=1032&u_aw=1920&u_cd=24&u_sd=1&dmc=8&adx=447&ady=4426&biw=1903&bih=945&scr_x=0&scr_y=654&eid=31090351%2C95352069%2C31090416%2C31090357%2C95347432%2C95350015&oid=2&psts=AOrYGsnmsAf5FgovMiyuoig_e6wjhOsMs_T9-R_sF1AGq8YEYa1WdOjxCwylSv1YJakskgg0owvLpyVX0WtsEgTxJ3Lt2cKPlC3S4v5nCFY&pvsid=2014775389331252&tmod=684137592&uas=3&nvt=1&ref=https%3A%2F%2Fphys.org%2F&fc=1920&brdim=0%2C0%2C0%2C0%2C1920%2C0%2C1920%2C1032%2C1920%2C945&vis=1&rsz=%7C%7CpeEbr%7C&abl=CS&pfx=0&fu=128&bc=31&bz=1&td=1&tdf=2&psd=W251bGwsbnVsbCxudWxsLDNd&nt=1&ifi=3&uci=a!3&btvi=3&fsb=1&dtd=22840

Simmetriya fizikada fundamental anlayışdır, keçmiş saysız-hesabsız tədqiqatlar fiziki sistemlərin bəzi spesifik xassələrinin birbaşa onların simmetriyalarından, məsələn, zamanın əksi və ya spin-fırlanma simmetriyalarından irəli gəldiyini və beləliklə asanlıqla proqnozlaşdırıla biləcəyini nümayiş etdirir. Yamilov və onun həmkarlarının topladığı tapıntılar simmetriyaların əhəmiyyətinin daha parlaq nümunəsini təqdim edir.

Skipetrov izah etdi: “Nəzərdə tutulan optik sistemin zamanın əks simmetriyasına malik olması və yeganə pozulmuş simmetriyanın translyasiya olması (bozukluğa görə) Andersonun ortoqonal universallıq sinfinə keçməsini şərtləndirir.

“Daha doğrusu, kritik nöqtənin yaxınlığında miqyaslama davranışının kəmiyyət təhlili kritik eksponentin ≈1.5-in ilk qiymətləndirilməsinə səbəb oldu. Onun dəyəri göstərir ki, bu keçid ortoqonal universallıq sinfinə aiddir və işıq lokalizasiyası ilə digər dalğa hadisələri, məsələn, pozulmuş elektronlar və ya səslər arasında dərin əlaqəni ortaya qoyur.”

Bu yaxınlarda aparılan araşdırma 3D-də işığın idarə edilməsinə yönəlmiş tədqiqatlar üçün tezliklə yeni imkanlar aça bilər. Komandanın simulyasiyalarında nümayiş etdirildiyi kimi, işığı təsadüfi strukturlarda məhdudlaşdırmaq bacarığı, məsələn, nanoməsaməli metallara əsaslana bilən optik cihazlar, sensorlar və lazerlər də daxil olmaqla yeni texnologiyaların inkişafına imkan verə bilər.

“Ən aktual istiqamət Anderson tərəfindən 3D metal sistemlərdə işığın lokalizasiyasının eksperimental yoxlanılmasıdır, lakin metalların optik udulması problem yaradır”, – Cao əlavə etdi.

“Yaxın IR və mikrodalğalı tezliklərə keçmək udulmanı azaldacaq. Biz keçidə necə təsir etdiyini başa düşmək üçün ədədi analizi idarə olunan absorbsiyaya malik sistemlərə genişləndirməyə çalışırıq. Bu, ideallaşdırılmış simulyasiyalarımızı real materiallarla əlaqələndirir və eksperimental dizaynı istiqamətləndirə bilər.”

Tədqiqatçılar növbəti tədqiqatlarında 3D metal sistemlərdə işığın Anderson lokalizasiyasını araşdırmağa davam etməyi planlaşdırırlar. Onlar həmçinin fotokatalizatorları və sensor cihazlarını inkişaf etdirə biləcək işıq-maddə qarşılıqlı təsirini artırmaq üçün nanoməsaməli metallarda işığın lokalizasiyasının necə istifadə oluna biləcəyinə diqqət yetirərək, bu keçidin real dünya tətbiqlərini araşdırmağı planlaşdırırlar.

Ətraflı məlumat: Aleksey Yamilov və başqaları, Anderson Transition for Light in a Thre-Dimensional Random Medium, Fiziki İcmal məktubları (2025). DOI: 10.1103/PhysRevLett.134.046302 . arXiv- də : DOI: 10.48550/arxiv.2408.04853

Jurnal məlumatı: Fiziki İcmal Məktubları , Təbiət Fizikası , arXiv   

© 2025 Science X Network