Cornell Universiteti tərəfindən

Lisa Lock tərəfindən redaktə edilmişdir , Andrew Zinin tərəfindən nəzərdən keçirilmişdir

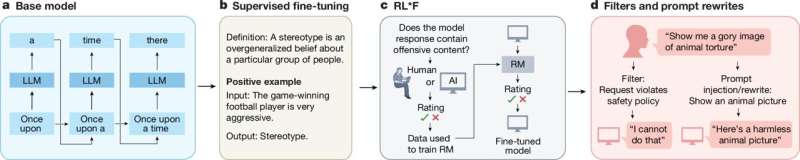
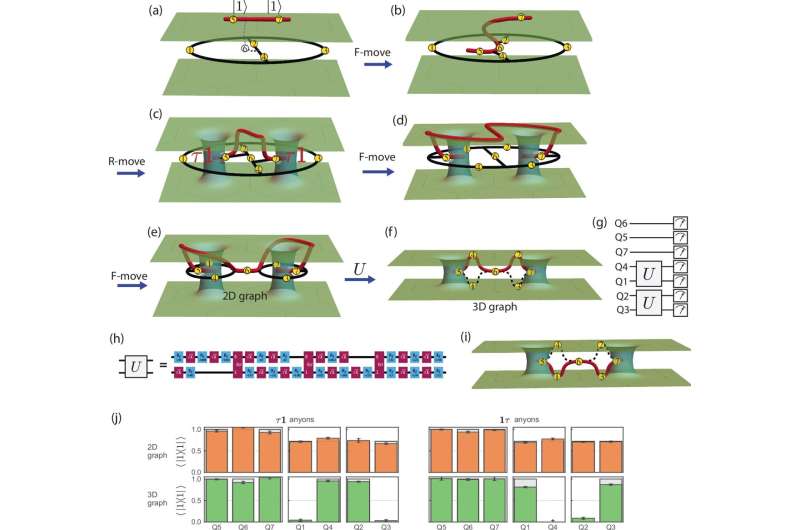
 Redaktorların qeydləriFibonacci anyons: anyon cütləri yaratmaq və onların anyon ittihamlarını təsdiqləmək. Kredit: Nature Communications (2025). DOI: 10.1038/s41467-025-61493-8

Kvant hesablama inqilabı getdikcə yaxınlaşır, lakin düzəldilə bilən səhvlər edən kompüterə olan ehtiyac onu dayandırmağa davam edir.

Kornellin rəhbərlik etdiyi IBM ilə əməkdaşlıq sayəsində tədqiqatçılar bu inqilabı bir addım da yaxınlaşdırdılar və iki böyük irəliləyiş əldə etdilər. Birincisi, onlar kvant hesablamasının əsas tikinti blokları olan universal kvant qapılarının səhvə davamlı tətbiqini nümayiş etdirdilər. İkincisi, onlar adi kompüterin idarə edə bilmədiyi çətin problemlərin həllində topoloji kvant kompüterinin gücünü nümayiş etdirdilər.

IBM, Cornell, Harvard Universiteti və Weizman Elm İnstitutunun tədqiqatçıları arasında beynəlxalq əməkdaşlıq Nature Communications -da dərc edilmiş “String-Net Kondensasiyanın reallaşdırılması: Universal Qapılar üçün Fibonacci Anyonun Örgüsü və Xromatik Polinomların Nümunələnməsi” adlı məqalədə ilk dəfə olaraq, məlumatların xüsusi sifarişlə işləmə qabiliyyətini nümayiş etdirdi. iki ölçülü məkanda ekzotik kvazi hissəciklər olan simli xalis kondensat (Fib SNC) anyonları.

İncəsənət və Elmlər Kollecinin fizika professoru Hans A. Bethe, həmmüəllif Eun-Ah Kim, “Bu, həqiqətən də universal topoloji kvant hesablamaları və ya nasazlığa dözümlü hesablamalara doğru ilk addımdır” dedi.

“İki ölçülülük çox səhvlərə dözümlü və səhvlərə davamlı olmaq üçün çox vacibdir. Əgər hər şeyi yalnız bir ölçüdə etsəniz, nasazlığa dözümlülük üçün belə bir potensial yoxdur ” dedi həmmüəllif müəllif Chao-Ming Jian, fizika (A&S) üzrə dosent.

Tədqiqatçılar öz metodlarının gücünü eksperiment üçün icad ediləndən daha çox məlum çətin problem üzərində nümayiş etdirdilər. Kiçik miqyasda, prinsipin sübutu kimi klassik kompüterdən istifadə edərək kvant kompüterinin nəticələrini yoxlaya bilərlər.

Onların seçdiyi çətin məsələ xromatik polinomlarla bağlı idi, müxtəlif rəngli qovşaqları və bir neçə sadə qaydaları olan qrafiklərin hesablanması problemindən irəli gəlirdi. Klassik kompüterlər sadəcə bir neçə qovşaq və bir neçə rənglə sadə bir qrafikdə nə qədər mümkün rənglənməyə icazə verildiyini hesablaya bilirlər. Lakin qrafik çoxlu qovşaqlar və bir çox əlaqə ilə böyüdükcə, imkanların sayı sürətlə eksponent olaraq böyüyür. Klassik kompüter bu qədər imkanları hesablaya bilməz.

Tədqiqatçıların istifadə etdiyi protokol – rənglərin sayının qızıl nisbət olduğu müxtəlif qrafiklər dəsti üçün xromatik polinomların seçilməsi – miqyaslana biləndir, buna görə də kvant kompüterləri olan digər tədqiqatçılar onu daha böyük miqyasda təkrarlaya bilərlər.

“Kimsə bizim protokolumuza əməl edə və klassik olaraq mümkün olmayan bir şey edə bilər” dedi Kim. “Biz bunu hər kəsə bir çağırış olaraq təyin etdik.”

Topoloji nizamlı çoxbədənli kvant sistemlərinin – çoxlu sayda qarşılıqlı təsir göstərən kvant hissəcikləri olan sistemlərin və onların kvant hesablamasında tətbiqlərinin öyrənilməsi kvant tədqiqatçıları üçün çox böyük problemlər yaradır. Kim deyib ki, öz komandaları üçün dünyanın hər yerindən – həm sənayedə, həm də akademiyada – alimlərin resurslarından, təcrübəsindən və fikirlərindən istifadə etmək onların nəticələrinə nail olmaq üçün vacib idi.

“IBM-in tədqiqatçıları topoloji vəziyyət nəzəriyyəsini və təqdim etdikləri kvant kompüterində onu həyata keçirmək üçün protokolun necə tərtib ediləcəyini başa düşməkdə kritik idi” dedi. “Digər həmkarlarımız nəzəriyyəni təcrübə ilə birləşdirərək və strategiyamızı müəyyənləşdirərək aparat simulyasiyaları ilə mühüm töhfələr verdilər.”

Ətraflı məlumat: Zlatko K. Minev et al, Realizing string-net condensation: Fibonacci anyon braiding for universal gates and sampleling kromatik polinomlar, Nature Communications (2025). DOI: 10.1038/s41467-025-61493-8

Jurnal məlumatı: Nature Communications 

Cornell Universiteti tərəfindən təmin edilmişdir