Krystal Kasal tərəfindən , Phys.org

redaktə edən: Gaby Clark , rəy verən: Robert Egan

 Redaktorların qeydləri

 GIST

Tercih edilən mənbə kimi əlavə edin

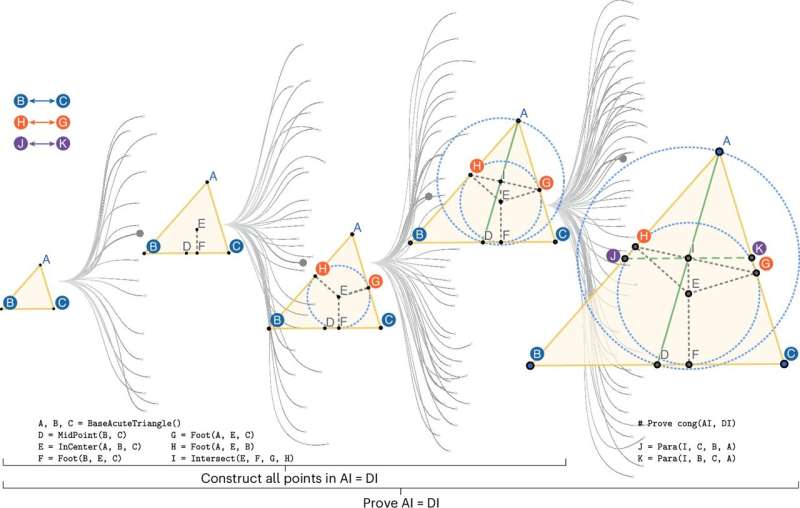
TongGeometry-nin simmetrik həndəsə probleminin yaradılması və həlli üçün idarə olunan ağac axtarışı. Mənbə: Nature Machine Intelligence (2026). DOI: 10.1038/s42256-025-01164-x

Beynəlxalq Riyaziyyat Olimpiadası (IMO) dünyanın hər yerindən istedadlı lisey şagirdlərinin iştirak etdiyi nüfuzlu bir yarışdır və iştirakçılar mürəkkəb riyazi məsələləri həll edirlər. Bu cür yarışlarda iştirak edən həndəsə məsələləri, xüsusən də formal məntiq və məkan düşüncəsi süni intellekt (Sİ) tədqiqatlarında vacib bir meyar kimi qeyd edilmişdir.

İndi Çində bir komanda bu olimpiada səviyyəli həndəsə problemlərini həm həll edə, həm də yarada bilən süni intellekt sistemi hazırlayıb. Yeni süni intellekt sistemi olan TongGeometry, dərin yaradıcılıq və düşüncə tələb edən bir sahədə insan olimpiadalarında ən yaxşı nəticələr göstərir. Onun nailiyyətləri tədqiqat qrupunun Nature Machine Intelligence jurnalında dərc olunmuş yeni tədqiqatında ətraflı şəkildə təsvir olunub .

Həndəsədə avtomatlaşdırılmış düşüncə

Bəzi süni intellekt sistemləri hazırda olimpiada səviyyəli həndəsə məsələlərini həll edə bilir, lakin onları təklif etmək üçün riyazi ustalıqla yanaşı, süni intellekt sistemlərində əldə etmək çətin olan estetik həssaslıq da tələb olunur. AlphaGeometry kimi əvvəlki sistemlər yalnız həll etməyə yönəlmişdi və yenə də əhəmiyyətli hesablama resursları tələb edirdi.

Tədqiqat müəllifləri yazırlar ki, “Ən çox heyranedici məsələlər aldadıcı sadəlik nümayiş etdirir: fundamental biliklər vasitəsilə əldə edilə bilən, lakin tam həllər üçün dərin yaradıcılıq tələb edən məsələlər. Riyazi zəriflik, xüsusən də müxtəlif formalarda simmetriya, nüfuzlu yarışlarda kritik keyfiyyət meyarı kimi xidmət edir.”

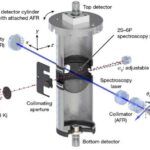
Həndəsənin vizual və konstruktiv təbiəti süni intellekt üçün maneələr yaradır. Tədqiqat müəlliflərinə görə, olimpiada həndəsə məsələlərinə hesablama yanaşmalarında fundamental məhdudiyyətlər “mühakimə yollarının kombinatorial partlayışı və evristik inkişaf üçün nümunəvi məsələlərin azlığı” səbəbindən yaranır.TongGeometry-nin həndəsi problemlərin həlli üçün aktyor-tənqidçi üslubunda neyron arxitekturası. Mənbə: Nature Machine Intelligence (2026). DOI: 10.1038/s42256-025-01164-x

TongGeometry: Olimpiada səviyyəli məsələ təklif edən və həll edən

Həndəsi mühakiməni modelləşdirmək üçün Markov çərçivəsi ilə idarə olunan ağac axtarışından istifadə edən neyro-simvolik sistem olan TongGeometry, bu həndəsə problemlərinin yaratdığı maneələri əsasən dəf etdiyi görünür. Komanda, sistemi iki böyük dil modelini – biri axtarış istiqamətlərini təklif edən, digəri isə mühakimə addımlarını qiymətləndirən modelləri – incə tənzimləməklə inkişaf etdirdi.

Əvvəlki yarışlardan 196 olimpiada məsələsini rəhbər statistika kimi istifadə edərək, sistem 6,7 milyard həndəsə məsələsindən ibarət depo yaratdı ki, bunlardan 4,1 milyardı riyazi simmetriya nümayiş etdirdi. Bu məsələlərdən üçü Çin və ABŞ-da keçirilən əsas riyaziyyat olimpiadaları üçün seçildi.

Tədqiqatçılar həmçinin TongGeometry-nin həll etmə qabiliyyətlərini AlphaGeometry (IMO-AG-30) üçün hazırlanmış məlumat dəsti və yeni məlumat dəsti (MO-TG-225) ilə sınaqdan keçirdilər və hər ikisi etalon kimi xidmət etdi. IMO-AG-30, 23 illik IMO yarışlarından 30 məsələni, MO-TG-225 isə Euler xətti teoremi kimi 225 məlum teoremi özündə birləşdirdi. TongGeometry, IMO-AG-30 etalonundakı bütün 30 məsələni həll edərək, bu xüsusi məlumat dəstində orta IMO qızıl medalçılarını üstələdi. Daha da təsirli olanı, bunu istehlakçı səviyyəli hesablama resurslarından istifadə edərək 38 dəqiqə ərzində etdi.

“TongGeometry-nin DD arxa planı, AlphaGeometry-nin DD+AR-ı ilə müqayisədə daha yaxşı problem həll etmə qabiliyyəti nümayiş etdirdi və ümumilikdə AlphaGeometry-yə yaxın performans səviyyələrinə çatdı. Qeyd etdik ki, AlphaGeometry-nin uğuru əsasən arxa plan mühərrikindən qaynaqlanır və ümumi həllərin 72,5%-i DD+AR tərəfindən əldə edilir.”

Tədqiqat müəllifləri izah edirlər ki, “Əksinə, TongGeometry yalnız problemlərin daha böyük bir hissəsini həll etməklə kifayətlənməyib (81,3% vs 45,3%), həm də köməkçi konstruksiya problemlərini həll etmək üçün neyron modellərindən daha effektiv şəkildə istifadə edib və problemlərin yalnız 55,2%-i təkbaşına DD tərəfindən həll edilib”.

Gündəlik məlumat üçün Phys.org-a etibar edən 100.000-dən çox abunəçi ilə elm, texnologiya və kosmosdakı ən son yenilikləri kəşf edin . Pulsuz bülletenimizə abunə olun və vacib olan nailiyyətlər, innovasiyalar və tədqiqatlar haqqında gündəlik və ya həftəlik yeniliklərdən xəbərdar olun .

Təhsil və tədqiqat potensialı

TongGeometry, cəbri və ya kombinatorial mühakimə tələb edən bütün mümkün həndəsə məsələlərini əhatə etməsə də, riyaziyyatın digər sahələrinə də şamil edilə bilər. Artıq təhsil müəssisələrində praktik tətbiqini nümayiş etdirib, burada təcrübəli IMO məşqçiləri məsələləri nəzərdən keçirir və düzəldir, sonra isə onları tələbələrlə birlikdə istifadə edirlər.

Müəlliflər yazır ki, “Bu seçilmiş kolleksiya daha sonra tələbələrə təqdim olunur və ikili məqsədə xidmət edir: tələbələrə mürəkkəb mövzuları və yarışlara xas texnikaları mənimsəməyə kömək edən zəngin təlim materialı mənbəyi təmin edir, eyni zamanda məşqçilər üçün güclü yaradıcı köməkçi rolunu oynayır və komandaları üçün maraqlı və çətin problemləri həll etməyə kömək edir”.

Müəlliflər həmçinin TongGeometry-nin tədqiqatlarda və hesablama həndəsəsi və riyaziyyat təhsilinin inkişafında istifadə potensialını qeyd edirlər.

Müəllifimiz Krystal Kasal tərəfindən sizin üçün yazılmış, Qeby Clark tərəfindən redaktə edilmiş və Robert Egan tərəfindən faktlar yoxlanılmış və nəzərdən keçirilmiş — bu məqalə diqqətli insan əməyinin nəticəsidir. Müstəqil elmi jurnalistikanı yaşatmaq üçün sizin kimi oxuculara güvənirik. Bu reportaj sizin üçün vacibdirsə, xahiş edirik ianə etməyi düşünün (xüsusilə aylıq). Təşəkkür olaraq reklamsız hesab əldə edəcəksiniz .

Nəşr detalları

Çi Çjan və digərləri, Rəhbərli ağac axtarışı ilə olimpiada həndəsəsinin təklif edilməsi və həlli, Təbiət Maşın Zəkası (2026). DOI: 10.1038/s42256-025-01164-x

Jurnal məlumatı: Təbiət Maşın Zəkası 

© 2026 Science X Network